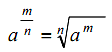เลขยกกำลัง

สมบัติของเลขยกกำลัง    

-สมบัติการคูณเลขยกกำลังที่มีเลขชี้กำลังเป็นจำนวนเต็มบวก เมื่อ a เป็นจำนวนใด ๆ และ m, n เป็นจำนวนเต็มบวก  

       

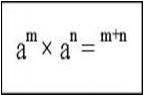
-เลขยกกำลังที่มีเลขชี้กำลังเป็นเศษส่วน

   

      เมื่อ a > 0 และ n เป็นจำนวนเต็มบวกที่มากกว่า 1

   

   

เมื่อ a ≠ 0 และ m เป็นจำนวนเต็มบวก ; n ≥ 2 ...อ่านเพิ่ม

การให้เหตุผลแบบนิรนัย

           การให้เหตุผลแบบนิรนัยเป็นวิธีการให้เหตุผลโดยสรุปผลจากข้อความซึ่งเป็นความจริงทั่วไปมาเป็นข้ออ้างเพื่อสนับสนุนให้เกิดข้อสรุปที่เป็นความรู้ใหม่ที่เป็นข้อสรุปส่วนย่อยข้อสรุปที่ได้จากการให้เหตุผล

แบบนิรนัยนั้นจะเป็นข้อสรุปที่อยู่ในขอบเขตของเหตุเท่านั้นจะเป็นข้อสรุปที่กว้างหรือเกินกว่าเหตุไม่ได้การให้เหตุผลแบบนิรนัยประกอบด้วยข้อความ2กลุ่มโดยข้อความกลุ่มแรกเป็นข้อความที่เป็นเหตุ เหตุอาจมี...อ่านเพิ่ม

การให้เหตุผลแบบอุปนัย

       การให้เหตุผลแบบอุปนัย (Inductive Reasoning) เกิดจากการที่มีสมมติฐานกรณีเฉพาะ หรือเหตุย่อยหลายๆ เหตุ เหตุย่อยแต่ละเหตุเป็นอิสระจากกัน มีความสำคัญเท่าๆ กัน และเหตุทั้งหลายเหล่านี้ไม่มีเหตุใดเหตุหนึ่งแสดงให้เห็นถึงความเป็นสมมติฐานกรณีทั่วไป หรือกล่าวได้ว่า การให้เหตุผลแบบอุปนัยคือการนำเหตุย่อยๆ แต่ละเหตุมารวมกัน เพื่อนำไปสู่ผลสรุปเป็นกรณีทั่วไป เช่นตัวอย่างการให้เหตุผลแบบอุปนัย...อ่านเพิ่ม

บทที่ 2

ระบบจำนวนจริง

สมบัติ	การบวก	การคูณ
ปิด	a+b €   R	ab  €   R
การสลับที่	a+ b = b+a	ab = ba
การเปลี่ยนหมู่	(a+b)+c = a+(b+c)	(ab)= a(bc)
การมีเอกลักษณ์	มีจำวนจริง 0 ซึ่ง0+a = a= a+0	มีจำนวนจ1 a = a= a  1 ริงซึ่ง 1 ซึ่ง
	เรียก 0ว่าเอกลักษณ์	เรียก 1 ว่าเอกลักษณ์
การมีอินเวอร์ส	สำหรับจำนวนจริง aจะมีจำนวนจริง –a  โดยที่ (-a)+a = 0 = a+(-a) เรียก –a ว่าอินเวอร์ส การบวกจำนวนจริงของ a	เรียก 1 ว่าเอกลักษณ์การคูณสำหรับจำนวนจริง a ที่ a   0 จะมีจำนวนจริง a  โดยที่ a a = 1 = a   a  เรียก a  ว่าอินเวอร์สการคูณของจำนวนจริงa
การแจกแจง	A(a+b) = ab+ac

อ่านเพิ่ม

บทที่ 1

เซต

2.1 เซต

เซต  เป็นคำที่ใช้บ่งบอกถึงกลุ่มของสิ่งต่างๆ และเมื่อกล่าวถึงกลุ่มใดแน่นอนว่าสิ่งใดอยู่ในกลุ่ม สิ่งใดไม่อยู่ในกลุ่ม เช่น

       เซตสระในภาษาอังกฤษ  หมายถึง  กลุ่มของอังกฤษ  a, e, i, o และ u

       เซตของจำนวนนับที่น้อยกว่า 10 หมายถึง  กลุ่มตัวเลข 1,2,3,4,5,6,7,8,และ9...อ่านเพิ่ม